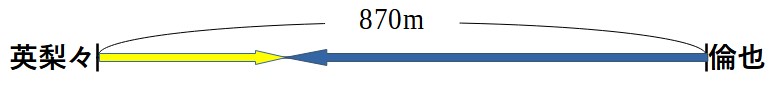歩幅と歩数の練習問題① 標準編
歩幅と歩数の標準問題
こちらは、歩幅と歩数の標準問題を載せているページです。
歩幅と歩数の詳しい解説はこちらへどうぞ。
歩幅と歩数の問題は、線分図を利用して速さの比を求める問題です。まず、線分図を書ける必要があります。 線分図の書き方がわからない方は、線分図の詳しい解説を読んでから戻ってきてください。
また、速さと比の関係を知っておく必要があります。不安な方は、速さと比の詳しい解説を読んでから戻ってきてください
それでは、まずは実際に線分図を書いて速さの比を求めてみましょう。
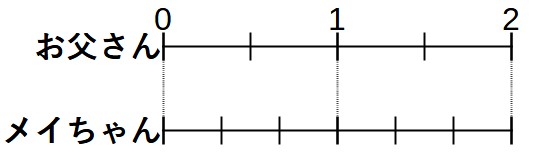
まずは歩幅に注目して線分図を書いてみます。2人の足がそろう場所を「0、1、2」として書いておくとわかりやすいです。
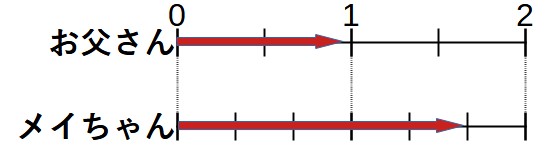
この線分図に、同じ時間でお父さんは2歩、メイちゃんは5歩歩くことを書き加えます。
時間が同じならば、道のりの比と速さの比は同じです。よって、上の線分図から、お父さんとメイちゃんの速さの比を求めることができます。
| 2 | : | 5 | |
| 2 | 3 |
=6:10
=3:5
(分数の比の計算方法はこちら)
よって答えは
3:5
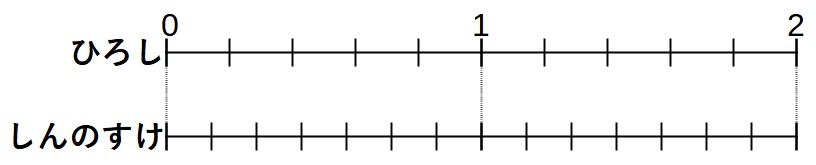
まずは歩幅に注目して線分図を書いてみます。2人の足がそろう場所を「0、1、2」として書いておくとわかりやすいです。
この線分図に、同じ時間でひろしさんは7歩、しんのすけさんは5歩歩くことを書き加えます。
時間が同じならば、道のりの比と速さの比は同じです。よって、上の線分図から、ひろしさんとしんのすけさんの速さの比を求めることができます。
| 7 | : | 5 | |
| 5 | 7 |
=49:25
よって答えは
49:25
歩幅と歩数の問題は、速さと比の問題と一緒に出題されることが多いです。
応用問題のように感じてしまうかもしれませんが、一つひとつ考えれば難しいことはまったくありません。実際に解いてみましょう。
英梨々さんと倫也くんはそれぞれの家を同時に出発し、英梨々さんは倫也くんの家に向かって、倫也くんは英梨々さんの家に向かって歩きます。
2人の家の間の道のりは870mです。2人が出会ったのは、英梨々さんの家から何mの地点でしょう。
問題文が長いので、まずは問題文をよく読んで状況を把握しましょう。歩幅と歩数や、速さと比や、旅人算の要素が入っていて、一見難しそうに感じるかもしれません。
実際には、一つひとつ考えていけばとても簡単です。
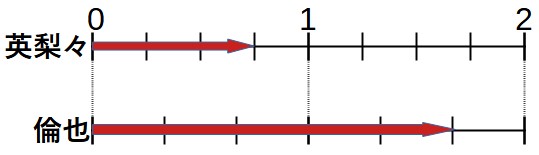
まずは英梨々さんと倫也くんの歩く速さの比を求めましょう。
時間が同じならば、道のりの比と速さの比は同じです。よって、上の線分図から、英梨々さんと倫也くんの歩く速さの比を求めることができます。
| 3 | : | 5 | |
| 4 | 3 |
これで、英梨々さんと友也くんの歩く速さの比が9:20であることがわかりました。
続いて、英梨々さんと倫也くんが出会った時の状況を線分図にしてみましょう。
英梨々さんが歩いた道のりと、倫也くんが歩いた道のりのそれぞれを求めることはできません。ですが、上の線分図を見ると、2人合わせて870m歩いたことがわかります。
さらに、2人は家を出てから出会うまで、同じ時間歩いたことになります(違う時間に出会うためにはタイムマシーンが必要です)。
時間が同じということは、2人の速さの比と、2人が歩いた道のりの比が同じになります。
英梨々さんと倫也くんの速さの比は9:20なので、歩いた道のりの比も9:20になります。
870mを9:20に分ければよいので、
| 870m | × | 9 | |
| 9+20 |
=270m
(比に分ける計算方法の解説はこちら)
求めたいのは、英梨々さんの家から2人が出会った地点までの道のりです。
よって答えは
270m
月火さんが朝7時50分に家を出てゆっくり歩いて学校へ行くと、始業時間の6分前に学校に到着しました。 火憐さんが朝8時00分に家を出て普通に歩いて学校へ行くと、始業時間の4分前に学校に到着しました。
月火さんが2歩歩く距離を、火憐さんは3歩で歩きます。月火さんが2歩歩く間に、火憐さんは7歩歩きます。
学校の始業時間は、午前何時何分でしょう。
問題文が長いので、まずは問題文をよく読んで状況を把握しましょう。いろいろな情報が入っていて、一見難しそうに感じるかもしれません。
実際には、一つひとつ考えていけばとても簡単です。
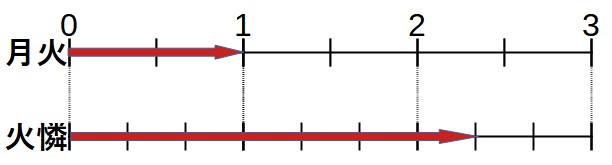
まずは月火さんと火憐さんの歩く速さの比を求めましょう。
時間が同じならば、道のりの比と速さの比は同じです。よって、上の線分図から、月火さんと火憐さんの歩く速さの比を求めることができます。
| 2 | : | 7 | |
| 2 | 3 |
=3:7
これで、月火さんと火憐さんの歩く速さの比が3:7であることがわかりました。
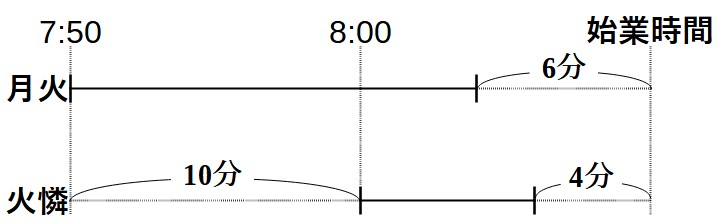
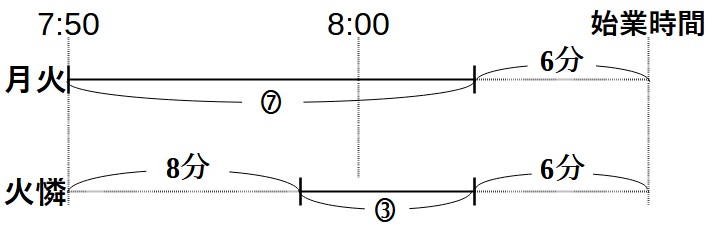
問題文には、時間に関する情報がたくさん出ています。整理するために、時間の線分図を書いてみます。
さて、2人とも家から学校へ行ったので、2人が歩いた道のりは同じです。
道のりが同じならば、速さの比と時間の比は逆比になります。
月火さんと火憐さんの速さの比は3:7だったので、歩いた時間の比は7:3になります。これを先ほどの線分図に書き加えます。
線分図が書けたら、比の数量(◯で囲ってある数字)と実際の時間が両方とも分かる区間を探します。ですが、このままではどちらも分かる区間はありません。
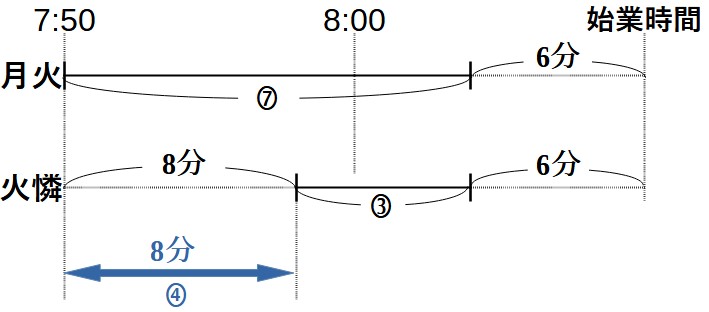
しかし、火憐さんの線分図を左に2分だけ左にずらせばうまくいきそうです。火憐さんの線分図を左に2分動かしてみましょう。
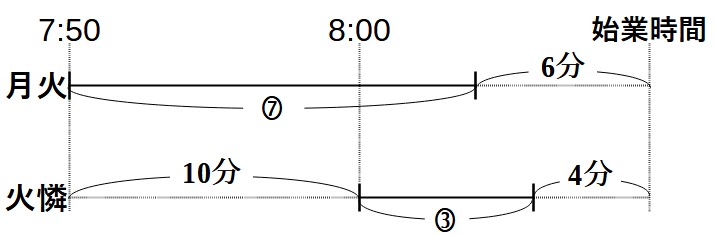
この状態であれば、比の数量と実際の時間が両方ともわかる区間があります。
上の線分図の青い矢印の区間に注目します。この区間は比の数量も実際の時間もわかります。
比
⑦-③
=④
時間
8分
これで、④が8分に当たることがわかりました。続いて、①が何分に当たるかを考えます。
8分÷④
=2分
これで、①が2分に当たることがわかりました。もう一度、元の線分図を見てみましょう。
線分図を見ると、火憐さんは朝8時00分に出発して、③だけ歩いて、始業時間の4分前に到着しています。このことから、始業時間を求めます。
午前8時00分+2分×③+4分
=午前8時10分
よって答えは
午前8時10分
どんなにいろいろな問題を混ぜても、歩幅と歩数の基本的な考え方が理解できていれば難しくありません。あせらず一つひとつ考えましょう。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!