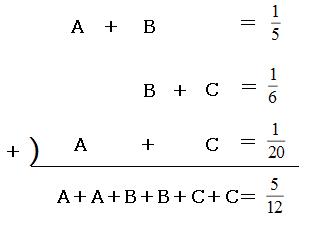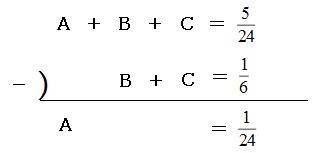仕事算の練習問題③ 応用編
仕事算の応用問題
こちらは、仕事算の応用問題を載せているページです。
仕事算の詳しい解説はこちら、基本問題はこちら、標準問題はこちらへどうぞ。
ひとりひとりの能力が違う場合は、仕事全体を①とします。みんなの能力が同じ場合は、1人がする仕事を①とします。
ひとりひとりの能力が違うので、仕事全体の量を①とします。
まずは、藍華さんと灯里さんそれぞれが1日で終わらせる仕事の量を求めましょう。
藍華さん
| ①÷15日 | = | 1 | |
| 15 |
灯里さん
| ①÷20日 | = | 1 | |
| 20 |
藍華さんと灯里さんがそれぞれ何日ずつ働いたかは分からないのですが、合計の日数は分かっています。このような場合は、つるかめ算を使うと便利です。
(つるかめ算の解説はこちら)
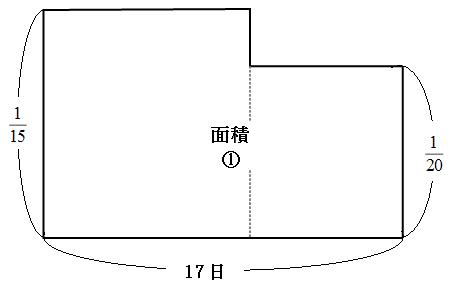
それでは早速面積図を書いていきましょう。
(面積図の書き方はこちら)
たて×よこ=面積
1日で終わらせる仕事の量×日数=仕事量
それでは、この面積図を使って考えていきましょう。
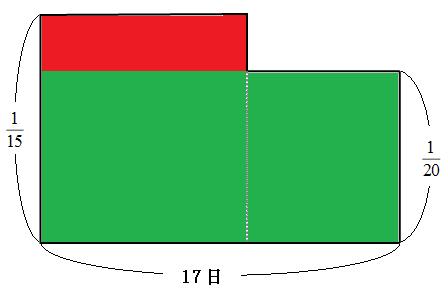
まずは、緑の部分の面積を求めます。
| 1 | ×17日= | 17 | |
| 20 | 20 |
全体の面積が①なので、赤い部分の面積は、
| ①- | 17 | = | 3 | |
| 20 | 20 |
また、赤い部分のたての長さは、
| 1 | - | 1 | = | 1 | |
| 15 | 20 | 60 |
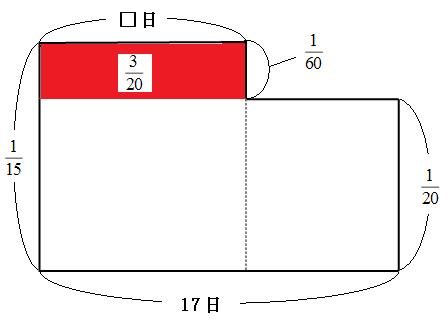
赤い部分に注目して面積図を見てみましょう。
上の図をもとに、赤い部分の横の長さを求めると、
| 3 | ÷ | 1 | = | 9 | |
| 20 | 60 |
よって、藍華さんが働いたのは9日間です。灯里さんが働いた日数は、
17日-9日=8日
よって答えは
8日
(1)この仕事を、A、B、Cの3人でやると、何時間何分かかるでしょう。
(2)この仕事をAだけでやると、何時間かかるでしょう。
(1)この仕事を、A、B、Cの3人でやると、何時間何分かかるでしょう。
ひとりひとりの能力が違うので、仕事全体の量を①とします。
まずはそれぞれの組合せが、1時間で終わらせる仕事の量を求めましょう。
A+B
| ①÷5時間 | = | 1 | |
| 5 |
B+C
| ①÷6時間 | = | 1 | |
| 6 |
A+C
| ①÷20時間 | = | 1 | |
| 20 |
これらを全て足してみます。
「=」より左側は、
(A+B)+(B+C)+(A+C)
=A+A+B+B+C+C
「=」より右側は、
| 1 | + | 1 | + | 1 | = | 25 | |
| 5 | 6 | 20 | 60 |
| = | 5 | ||
| 12 |
よって、Aが2人とBが2人とCが2人で仕事をすると、
| 1時間で | 5 | 終わる | ||
| 12 |
実際にはAもBもCも1人ずつしかいないので(分身の術が使えれば話は別)、1時間でできる仕事の量は半分。
| 5 | ÷2= | 5 | |
| 12 | 24 |
なので、3人で働いて①の仕事を終わらせるのにかかる時間は、
| ①÷ | 5 | = | 24 | |
| 24 | 5 |
| = | 4 | 4 | ||
| 5 |
| 4 | 4 | 時間= | 4時間48分 | |
| 5 |
よって答えは
4時間48分
(2)この仕事をAだけでやると、何時間かかるでしょう。
Aが1時間に終わらせる仕事量を求めるために、3人で仕事をした時の仕事量から、「B+C」の仕事量を引きます。
「=」より左側は、
(A+B+C)-(B+C)=A
「=」より右側は、
| 5 | - | 1 | = | 1 | |
| 24 | 6 | 24 |
なので、Aが1人で①の仕事を終わらせるのにかかる時間は、
| ①÷ | 1 | = | 24 | |
| 24 |
よって答えは
24時間
仕事には適度な休憩を!!
ひとりひとりの能力が違うので、仕事全体の量を①とします。
とりあえず、線分図に書いて考えてみようと思います。まずは状況をまとめます。
今井さんが2時間休むと8時間で終わる。
滝沢さん→8時間働く
今井さん→6時間働く
滝沢さんが8時間休むと12時間で終わる。
滝沢さん→4時間働く
今井さん→12時間働く
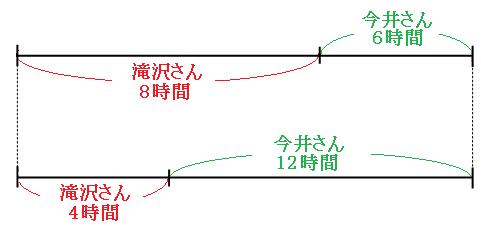
それでは線分図を書いてみます。全体の仕事量は同じなので、線分図の全体の長さは同じにしておきます。
この2本の線分図を見比べてみましょう。
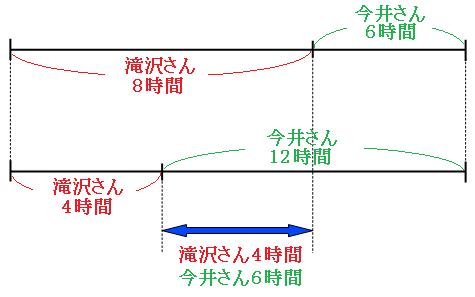
上の図のように、青い矢印の部分に注目してみましょう。滝沢さんに注目して青い部分を求め、続いて、今井さんに注目して青い部分を求めます。
滝沢さん
8時間-4時間=4時間
今井さん
12時間-6時間=6時間
つまり、滝沢さんが4時間で終わらせる仕事の量と、今井さんが6時間で終わらせる仕事の量は同じです。
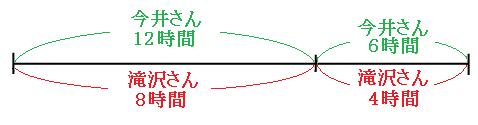
これを利用して、上の線分図にもう少し書き加えてみましょう。今井さん6時間の部分に滝沢さん4時間を書き加えます。
また、滝沢さんが8時間で終わらせる仕事の量を、今井さんは12時間で終わらせるので、滝沢さん8時間の部分に今井さん12時間を書き加えます。
線分図より、この仕事を滝沢さん1人でやると12時間、今井さん1人でやると18時間かかることがわかりました。
よって、それぞれが1時間で終わらせる仕事の量は、
滝沢さん
| ① | ÷12時間= | 1 | |
| 12 |
今井さん
| ① | ÷18時間= | 1 | |
| 18 |
滝沢さん+今井さん
| 1 | + | 1 | = | 5 | |
| 12 | 18 | 36 |
なので、滝沢さんと今井さんが2人で働いて、①の仕事を終わらせるのにかかる時間は、
| ① | ÷ | 5 | = | 36 | |
| 36 | 5 |
| = | 7 | 1 | ||
| 5 |
| 7 | 1 | 時間= | 7時間12分 | |
| 5 |
よって答えは
7時間12分
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!