過不足算
過不足算とは
過不足算とは、ある個数の物を2種類の方法で配った時に、○個余ったり、□個足りなくなったりする問題です。 線分図を書いて解く人と、面積図を書いて解く人がいますが、ここでは面積図を使った解き方を解説していきます。 面積図を書くことにある程度慣れている人ならば、面積図を使ったほうが楽だと思います。
過不足算の解き方
面積図を使って過不足算を解く場合、たてを1人あたりに配る個数、横を人数、面積を個数と置きかえます。
たて×よこ=面積
1人あたりの個数×人数=個数
面積図が少しごちゃごちゃしてしまうので、慣れるまでは難しく感じるかもしれません。 ですが、書き方も読み方もほぼワンパターンですので、あきらめずに練習して、できるようにしてください。
「足りなかった」や「余った」と書いてあるので、これは過不足算の問題です。面積図をかいていきます。 たてを1人の金額、横を人数、面積を合計の金額に置きかえます。
たて×よこ=面積
1人の金額×人数=合計の金額
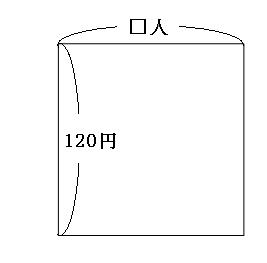
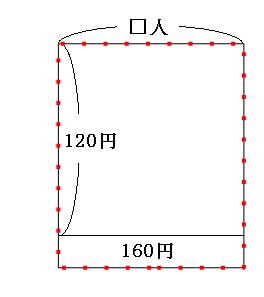
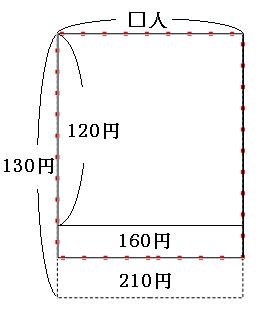
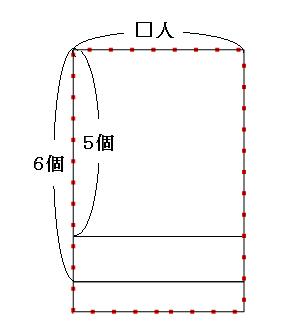
まずは、「1人120円ずつ集めると160円足りなかった」の面積図をかいていきます。 クラスの人数を□人として、1人120円ずつ、□人から集めてみましょう。クラスの人数はわからないので、横の長さは適当に書いておきます。
これでは160円足りなかったということは、プレゼントの値段はこれよりも160円高かったということになります。 なので、今書いた面積図に、あと160円面積を足してみましょう。
赤い点線の長方形の面積が、プレゼントの値段です。
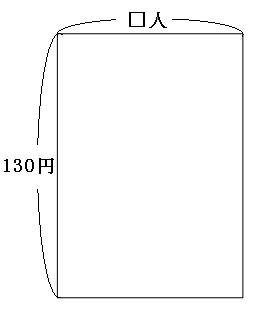
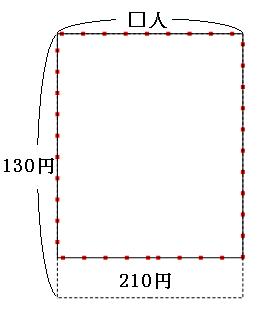
続けて、「1人130円ずつ集めたら210円余った」の面積図も書いてみます。
まずは、1人130円ずつ、□人から集めてみます。
これでは210円余ったということは、プレゼントの値段はこれよりも210円安かったということになります。 なので、今書いた面積図を、ここから210円分小さくしてみましょう。
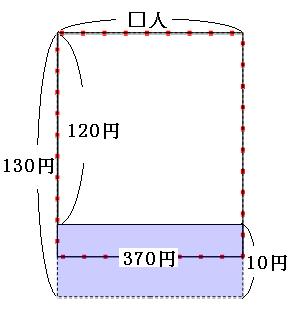
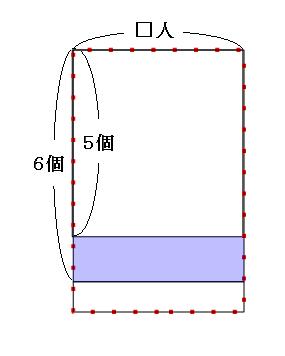
赤い点線の長方形の面積がプレゼントの値段です。 それでは、さっき書いた「1人120円づつ集めると160円足りなかった」面積図と重ねてみましょう。
どちらの面積図も、プレゼントの値段は同じなので、赤い点線の長方形の部分はピッタリと一致します。 この面積図の中に、面積もたての長さも両方ともわかる部分がないか探します。
青い長形の部分に注目すると、
たて→130円-120円=10円
面積→160円+210円=370円
なので、たてが10円、横が□人、面積が370円だということがわかりました。よって、
□=370÷10=37
これで、横の長さが37人であることがわかりました。横をクラスの人数に設定していましたので、クラスの人数は37人です。
続いてプレゼントの値段を出しますが、これはどちらのヒントを使って考えても大丈夫です。
今回は「1人120円ずつ集めると160円足りない」の方を使ってみます。
120円×37人+160円=4440円+160円
=4600円
よっと答えは
クラスの人数…37人、プレゼントの値段…4600円
どうでしょう。面積図が少し複雑でしたね。コツは、例題の中でも黄色マーカーが引いてありますが、「どちらで考えてもプレゼントの値段は同じなので、この部分が重なるように書く」ことです。
例題1のように、「余ったり足りなかったりする問題」がほとんどですが、「どちらも足りない」場合や、「どちらも余る」場合もあります。が、やることはまったく同じですので安心してください。
「余った」と書いてあるので、これは過不足算の問題です。面積図をかいていきます。 たてを1人に配るお菓子の個数、横を人数、面積をお菓子の個数に置きかえます。
たて×よこ=面積
1人の個数×人数=合計の個数
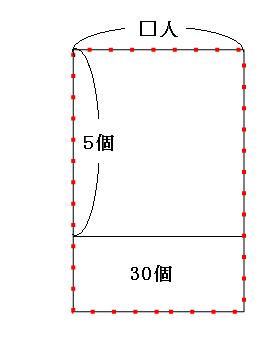
まずは、「1人に5個ずつ配ると30個余る」の面積図をかいていきます。 子供の人数を□人とします。子供の人数はわからないので、横の長さは適当に書いておきます。
赤い点線の長方形の面積が、お菓子全部の個数です。続いて「1人に6個ずつ配ると10個余る」の線分図を書いてみます。
赤い点線の長方形の面積が、お菓子全部の個数です。それでは、ふたつの面積図を重ねてみます。
どちらの面積図も、お菓子全部の個数は同じなので、赤い点線の長方形の部分はピッタリと一致します。 この面積図の中に、面積もたての長さも両方ともわかる部分がないか探します。
少し見にくいのですが、青い長形の部分に注目すると、
たて→6個-5個=1個
面積→30個-10個=20個
なので、たてが1個、横が□人、面積が20個だということがわかりました。よって、
□=20÷1=20
これで、横の長さが20人であることがわかりました。横をラジオ体操に来た子供の人数に設定していましたので、子供の人数は20人です。
続いてお菓子全部の個数を求めます。
5個×20人+30個=130個
よっと答えは
子供の人数…20人、お菓子…130個
「どちらも余る」や「どちらも足りない」の場合は、面積が重なってしまって少し見にくいと思います。
どの部分の面積がいくつなのか、ていねいに考えて解いてください。
長いすの過不足算の解き方
過不足算といえばもうひとつ、長いす系の問題があります。座る場所が余ったり足りなかったりするお話なので、これは過不足算の問題です。面積図をかいていきます。 たてを1つの長いすに座る人数、横をいすの数、面積を生徒の人数に置きかえます。
たて×よこ=面積
1つに座る人数×長いすの数=座っている生徒の人数
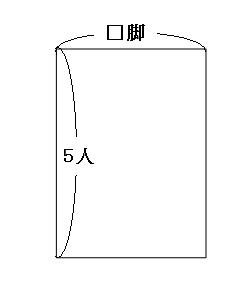
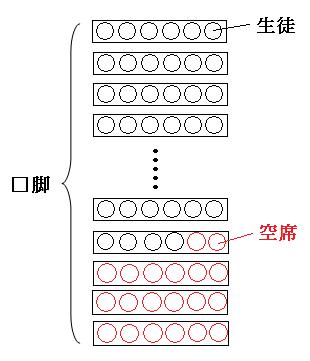
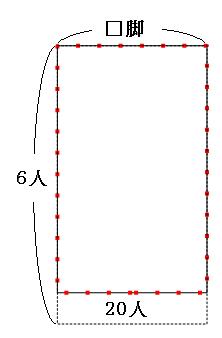
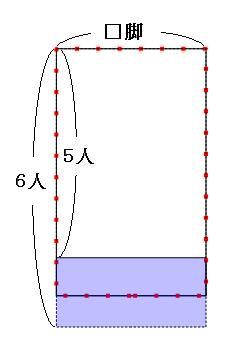
まずは、「5人ずつ座ると30人が座れない」の面積図をかいていきます。まずは、座っている生徒の面積図をかいてみます。 いすの数を□脚とします。いすの数はわからないので、横の長さは適当に書いておきます。
「30人が座れなかった」と書いてあるので、実際には生徒はもう30人いたということになります。なので、今書いた線分図に30人足しておきます。
赤い点線の長方形の面積が、生徒全員の人数です。
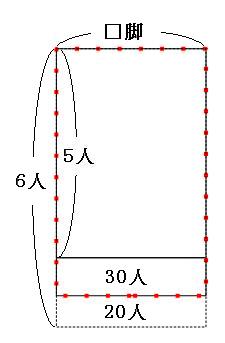
続いて「6人ずつ座ると4人だけ座る長いすが1脚でき、1人も座らない長いすが3脚できる」の線分図を書いてみますが、面積図を書く前に、まずは状況を整理しておきます。
続けて面積図を書きます。まずは、「もしもいすが全部生徒で埋まったら」の面積図を書きます。
しかし実際には空席が20席あったので、生徒の数はこれよりも20人少なかったということになります。なので、今書いた線分図から20人引いておきます。
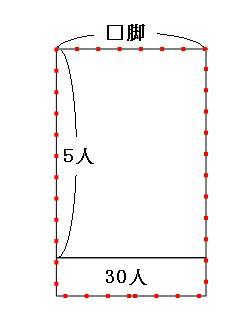
赤い点線の長方形の面積が、生徒全員の人数です。それでは、ふたつの面積図を重ねてみます。
どちらの面積図も、生徒の人数は同じなので、赤い点線の長方形の部分はピッタリと一致します。 この面積図の中に、面積もたての長さも両方ともわかる部分がないか探します。
青い長形の部分に注目すると、
たて→6人-5人=1人
面積→30人+20人=50人
なので、たてが1人、横が□脚、面積が50人だということがわかりました。よって、
□=50÷1=50
これで、横の長さが50脚であることがわかりました。横を長いすの数に設定していましたので、長いすは50脚です。
続いて生徒の人数を求めます。
5人×50脚+30人=280人
よっと答えは
長いす…50脚、生徒…280人
このように、長いす系の問題はいすが余ったりするので、こんがらがってしまう人も多いようです。 頭の中で状況を理解できなければ、絵を描いて、席が何人分空いているの考えましょう。それでは過不足算をまとめます。
面積図のメインパートはここまでです。おまけ的な感じで、もう少し面積図続きます。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!