基本 速さ
速さとは
速さとは、一定時間に進む道のりのことです。
1時間で60㎞進むのならば、時速60㎞と表されます。毎時60㎞や60㎞/時(60km毎時)などと表されることもあります。
1分間で30m進むのならば分速30m、1秒間に10km進むのならば秒速10㎞となります。
速さの解き方
速さの問題には3つの要素があります。「道のり」「速さ」「時間」です。それぞれの頭文字をとって、「みはじ」と言われます。
この3つの要素の中の2つがわかっていれば、もう1つは計算で求められます。
速さの計算が苦手という話を聞きますが、先ほど説明した「速さとは何か」をしっかり理解していればそれほど難しくありません。
さっそく「道のり」「速さ」「時間」の3つの要素の求め方を考えてみましょう。
道のりの求め方
「速さ」と「時間」がわかっていれば、「道のり」は簡単に求められます。次の例題を使って考えてみましょう。
「何kmでしょう。」と聞かれているので、道のりを求めます。
「道のり」「速さ」「時間」の3つの要素のうち、「速さ」と「時間」がわかっています。
ですので、「速さとは何か」を考えれば「道のり」を求めることができます。
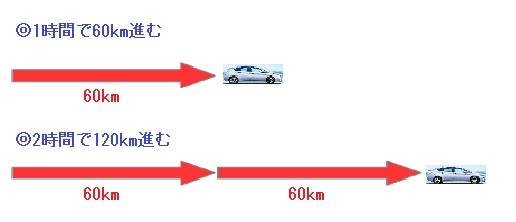
時速60kmとは、1時間に60km進む速さのことです。
上の絵のように、1時間で60km進むのであれば、2時間であれば2倍の120km進むはずです。
これを式で表すと、
60×2=120
よって答えは
120km
道のりの求め方はイメージしやすいと思います。
公式にすると、
道のり=速さ×時間
速さの求め方
「道のり」と「時間」がわかっていれば、「速さ」は簡単に求められます。次の例題を使って考えてみましょう。
「走った速さは分速何mでしょう。」と聞かれているので、速さを求めます。
「道のり」「速さ」「時間」の3つの要素のうち、「道のり」と「時間」がわかっています。
ですので、「速さとは何か」を考えれば「速さ」を求めることができます。
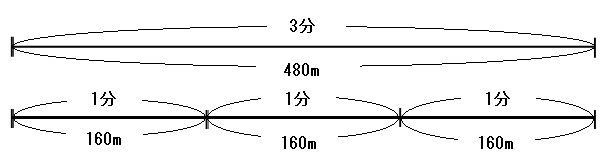
分速○mとは、1分間に○m進む速さのことです。
上の絵のように、3分間で480m進むのであれば、1分で160mずつ進んだはずです。
これを式で表すと、
480÷3=160
よって答えは
分速160m
どうでしょう。道のりの求めるときよりは少し難しいですね。
速さの考え方を身につける良いトレーニングになりますので、練習問題をたくさん解いてください。
ちなみに公式にすると、
速さ=道のり÷時間
時間の求め方
「道のり」と「速さ」がわかっていれば、「時間」は簡単に求められます。次の例題を使って考えてみましょう。
「何秒かかるでしょう。」と聞かれているので、時間を求めます。
「道のり」「速さ」「時間」の3つの要素のうち、「道のり」と「速さ」がわかっています。
ですので、「速さとは何か」を考えれば「時間」を求めることができます。
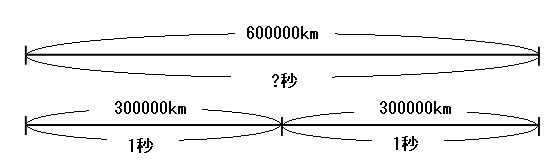
秒速300000kmとは、1秒間に300000km進む速さのことです。
上の絵のように、1秒間で300000km進むのであれば、600000km進むのには2秒かかるはずです。
これを式で表すと、
600000÷300000=2
よって答えは
2秒
どうでしょう。初めて解く場合はこれも少し難しいかもしれません。
ですが、「速さとは何か」をいつも考えながら練習すれば、すぐにできるようになるはずです。
ちなみに公式にすると、
時間=道のり÷速さ
速さの計算問題の魔法の図
この図はみなさん見たことがあるでしょう。「みはじ」と覚えていると思います。
「み」は「道のり」、「は」は「速さ」、「じ」は「時間」を示しています。
「道のり」を「きょり」として、「きはじ」と覚えている人もいるかもしれません。
道のりを求めたい時は「み」の部分を隠して、速さ×時間となります。求めたい部分を隠して使います。
すると、先ほど考えた公式の通り、
道のり=速さ×時間
速さ=道のり÷時間
時間=道のり÷速さ
と、なります。
実際の試験では時間制限があり、基本的なことをいちいち考えている時間はありません。
また、数字が複雑になると「あれ?どうするんだっけ?」と迷ってしまうこともあります。
時間短縮のためにも「みはじの図」にたよってしまうと良いでしょう。
頭の中で思い浮かべるよりも、実際に書いてみて、手で隠しながら式を作った方が簡単です。速さの問題が出たら、問題用紙のはしに「みはじの図」を書いておくと良いでしょう。
ただし、最初は必ず「速さとは何か」をしっかり考えながら練習してください。図にたよりすぎると、応用問題に対応できなくなってしまいます。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!