ニュートン算の解き方は2パターン!ニュートン算の苦手は克服できる!
ニュートン算とは
ニュートン算とは、とある行列にどんどん人が並んでいく中で、どれくらいの時間で行列をなくすことができるかを求める問題です。 行列の人が、水や草に置きかえられることもあります。仕事算や旅人算の考え方と合わせて、応用されることが多いです。 出題のパターンも非常に多く、応用力を試されることも多い問題なので、苦労することもあるかもしれません。 ここでは基本の部分を解説しようと思います。ここをしっかりと定着させて、応用問題に備えましょう。 基本の出題パターンは2種類です。
- 行列の最初の状況がわかっている。
- 行列の最初の状況がわかっていない。
行列の最初の状況がわかっているニュートン算の解き方
行列の最初の状況がわかっているときは、旅人算のように1分後の状況を考えるとわかりやすいと思います。
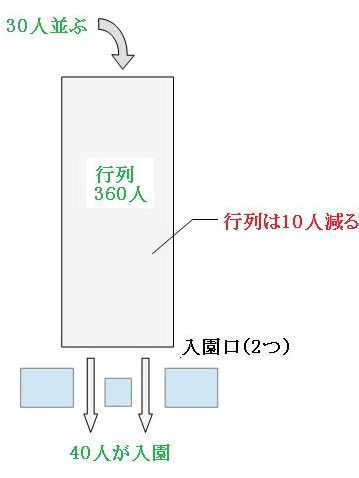
行列が最初360人であることがわかっているので、旅人算のように1分後のことを考えます。入園口が2個のときは36分で行列がなくなったので、1分あたりに減った行列の人数を求めると、
360人÷36分=10人
よって、1分で10人ずつ行列から人が減っていくことになります。 列は1分で30人ずつ増えていくのに、実際には10人ずつ減っていたということは、この1分で40人が入園していったことになります。最初の1分間の状況を図で書くと、下のようになります。
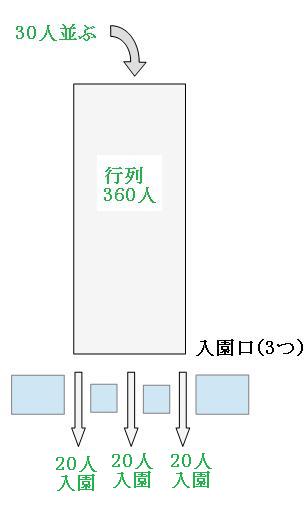
2個の入園口から40人入園したので、1個あたり20人入園したことになります。では、入園口が3個のときも、最初の1分間の状況を考えてみましょう。
1個の入園口から20人入園するので、3個の入園口から入園する人数を求めると
20人×3個=60人
つまり、最初の1分で行列に30人並び、60人が入園していきました。よって、この1分間で行列は30人減ったことになります。 全部で360人減らさなければならないので、それまでにかかった時間を求めると、
360÷30=12
よって答えは
12分
パンダも良いですが、ペンギンが一番好きです。
最初の状況がわかっているのなら、1分後の状況をしっかりと考えられれば難しくありません。絵や図を書いて、ゆっくり考えてみましょう。
行列の最初の状況がわかっていないニュートン算の解き方
行列の最初の状況がわからないときは、線分図を書いて考えるのが一般的です。 いろいろなタイプの問題があるのですが、そのほとんどは今回解説する線分図でなんとかなると思います。
水そうに最初に何L入っているかがわかリません。最初の状況がわからない場合は線分図を書いて考えるのですが、その前に、水そうが空になるまでにしたポンプの仕事を考えてみましょう。
1個のポンプが1分間にする仕事を①とすると
◎ポンプ3個で水を抜いたとき
①×3個×10分=㉚
◎ポンプ5個で水を抜くとき
①×5個×4分=⑳
また、水そうに入ってくる水の量は
◎ポンプ3個で水を抜いたとき
毎分5L×10分=50L
◎ポンプ5個で水を抜くとき
毎分5L×4分=20L
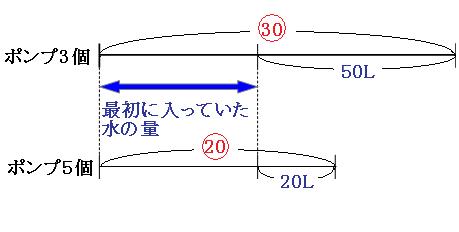
以上のことを線分図に書き込むと、下のようになります。
この線分図を見比べてみると
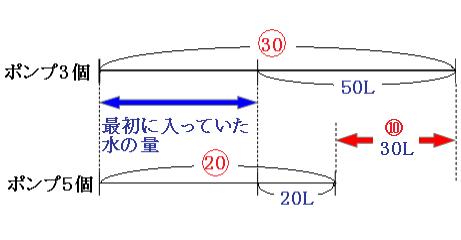
図のように、⑩にあたる部分が30Lとなっています。よって
30L÷⑩=3L
で、①が3Lにあたることがわかりました。
これをもとに、線分図を見てみましょう。どちらの線分図で考えても大丈夫です。今回は上の線分図を使って考えてみましょう。
線分図を見ると、最初に入っていた水の量は「㉚-50L」にあたります。①が3Lにあたるので、
3L×㉚-50L
=90L-50L
=40L
よって答えは
40L
この問題を見るたびに、「なんて無駄なことをしているんだろう・・・。」と思います。それではニュートン算をまとめます。
いろいろな考え方が混ざっているので、図や絵を書いてみてもわからなければ、もう一度仕事算や旅人算をしっかり復習してからトライしてみてください。 次は話がガラッと変わって、数列のお話です。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!