比の練習問題② 標準編
比の標準問題
こちらは、比の標準問題を載せているページです。
比の詳しい解説はこちら、基本問題はこちら、応用問題はこちらへどうぞ。
3人の体重の合計が178kgのとき、日向くんの体重は何kgでしょう。
まずは、3人の連比を求めましょう。今回はどちらの比にも影山くんが入っていますので、影山くんを「33」と「11」の最小公倍数の「33」でそろえましょう。
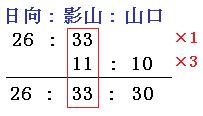
よって、日向くんと影山くんと山口くんの体重の比は、26:33:30です。
3人の体重の合計は178kgですので、日向くんの体重は、178kgを26:33:30に分けたうちの「26」の部分です。(分ける比の計算方法はこちら)
178kg÷(26+33+30)×26
=178÷89×26
=52kg
よって答えは
52kg
まずは、3つの角の連比を求めましょう。

よって、角A:角B:角C=2:3:4です。三角形の内角の和が180°であることを使って、それぞれの角の大きさを求めていきます。
角A
180°÷(2+3+4)×2
=40°
角B
180°÷(2+3+4)×3
=60°
角c
180°-(40°+60°)
=80°
よって答えは
角A=40°、角B=60°、角C=80°
(1)ニンジンとたまねぎとじゃがいもの代金の比を求めましょう。
(2)ニンジン1本、たまねぎ2個、じゃがいも3個の代金の合計が200円のとき、じゃがいもは1個の値段はいくらでしょう。
(1)ニンジンとたまねぎとじゃがいもの代金の比を求めましょう。
普通、1個の値段と買った個数をかけ算すると代金を求めることができます。今回は実際の値段も個数も分かっていないのですが、比の場合でも同じようにかけ算をしてしまって大丈夫です。 なので、ニンジンとたまねぎとじゃがいもの代金の比は、
(2×1):(3×2):(4×2)
=2:6:8
=1:3:4
よって答えは
1:3:4
(2)ニンジン1本、たまねぎ2個、じゃがいも3個の代金の合計が200円のとき、じゃがいもは1個の値段はいくらでしょう。
ニンジン1本、たまねぎ2個、じゃがいも3個の代金の比は、
(2×1):(3×2):(4×3)
=2:6:12
=1:3:6
つまり、じゃがいも3個の代金は、200円を1:3:6に分けたうちの「6」の部分になります。(分ける比の計算方法はこちら)
200円÷(1+3+6)×6
=200÷10×6
=120
じゃがいも3個の値段が120円なので、じゃがいも1個の値段は、
120円÷3個=40円
よって答えは
40円
カレーはとても美味しいものだと思います。
比例式を作って考えます。比例式を作るときは、順番に気をつけてください。今回は「メガネをかけている:メガネをかけていない」の順番で作っていきます。(比例式の計算方法はこちら)
5:13=10人:a
5×a=13×10
5×a=130
a=130÷5
a=26
よって答えは
26人
メガネ大事です。
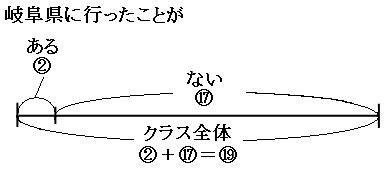
岐阜県に行ったことがある人の人数と、クラス全体の人数の比は2:19です。
それでは比例式を作りましょう。今回は「岐阜県に行ったことがある:クラス全体」の順番で作っていきます。
2:19=4人:a
2×a=19×4
2×a=76
a=76÷2
a=38
よって答えは
38人
(1)スイカとメロンの個数の比を求めましょう。
(2)スイカとメロンすべての重さは、全部で何kgでしょう。
(1)スイカとメロンの個数の比を求めましょう。
普通、全体の重さを1個の重さでわり算すると、個数が求められます。今回は実際の全体の重さは分かっていないのですが、比の場合でも同じようにわり算をして大丈夫です。 なので、スイカとメロンの個数の比は、
(4÷6kg):(1÷1kg)
| = | 4 | :1 | ||||
| 6 |
=4:6
=2:3
よって答えは
2:3
(2)スイカとメロンすべての重さは、全部で何kgでしょう。
スイカとメロンのそれぞれの個数を求めましょう。
スイカ
20個÷(2+3)×2
=20個÷5×2
=8個
メロン
20個-8個=12個
スイカとメロンすべての重さは、
6kg×8個+1kg×12個
=48+12
=60
よって答えは
60kg
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!