通過算の練習問題② 標準編
通過算の標準問題
こちらは、通過算の標準問題を載せているページです。
通過算の詳しい解説はこちら、基本問題はこちら、応用問題はこちらへどうぞ。
通過算のポイントは、絵を描いて、実際に走った道のりを求めることです。
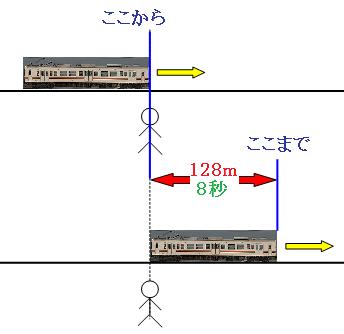
列車の先頭が自分の前にやって来た時と、列車の最後尾が自分を通り過ぎた時の絵を描いて、列車が進んだ道のりを考えます。列車は左から右へ進むとします。
図のように、自分の前を通りすぎるのに、列車は、列車の長さ分の128m進みます。かかった時間は8秒なので、速さは、
128m÷8秒＝秒速16m
よって答えは
秒速16m
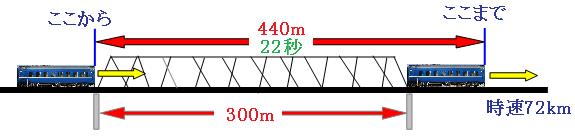
列車が走った道のりを求めると、
時速72km×22秒
＝秒速20m×22秒
＝440m
（速さの単位変換の方法はこちら）
列車が鉄橋をわたり始めた時と、列車の最後尾が鉄橋をわたり終わった時の絵を描いて、列車が進んだ道のりを考えます。列車は左から右へ進むとします。
この図より、列車の長さは、
440m－300m＝140m
よって答えは
140m
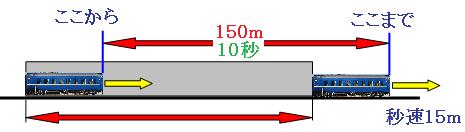
列車が走った道のりを求めると、
秒速15m×10秒＝150m
列車がトンネルに完全に入った時と、列車の最後尾がトンネルを完全に出終わる時の絵を描いて、列車が進んだ道のりを考えます。列車は左から右へ進むとします。
この図を見ると、列車が走った道のりとトンネルの長さは同じになっています。
よって答えは
150m
列車の長さもトンネルの長さも両方分からないので、「これで出せるのかな？」とも思うのですが、絵を描いてみるとなんてことはありません。
「あれ？」と思っても、できるところまで計算したり、絵を描いてみるとなんとかなったりしますので、頭の中で考えてばかりではなく、しっかりと紙に書いて考えてみましょう。
意外とスラっと解けたりすることもありますよ！
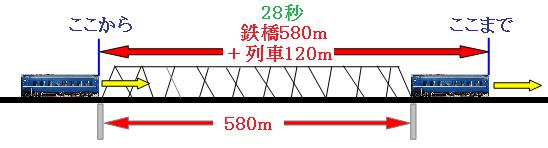
鉄橋の話とトンネルの話を、別々に考えます。まずは鉄橋の話を考えましょう。
列車が鉄橋をわたり始めた時と、列車の最後尾が鉄橋をわたり終わった時の絵を描いて、列車が進んだ道のりを考えます。
この図より、列車が進んだ道のりは、
580m＋120m＝700m
700mを28秒で進んだので、列車の速さは、
700m÷28秒＝秒速25m
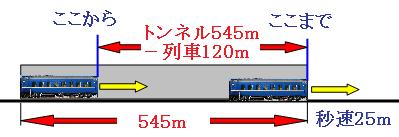
続いてトンネルの話を考えます。
列車がトンネルに完全に入った時と、列車の先頭がトンネルの出口に来た時の絵を描いて、列車が進んだ道のりを考えます。
この図より、列車が進んだ道のりは、
545m－120m＝425m
秒速25mで425mを進むのにかかる時間は、
425m÷秒速25m＝17秒
よって答えは
17秒
たくさん絵を描いてください。
