合同と相似
合同とは
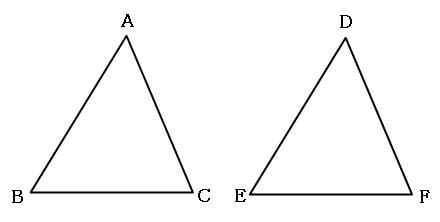
合同とは、形も大きさも同じ図形のことです。
上の三角形ABCと三角形DEFは、形も大きさも同じなので合同です。「三角形ABCと三角形DEFは合同」といいます。
「頂点Aと頂点D」や、「角Bと角E」、「辺ABと辺DE」など、組となる部分を「対応する」といいます。
当たり前なのですが、形も大きさも同じなので、対応する角の大きさや、対応する辺の長さは同じです。
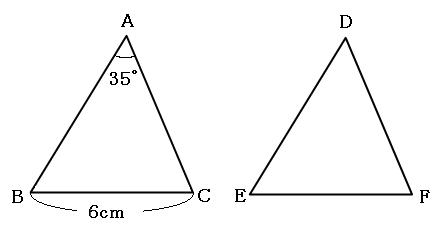
ふたつの三角形は合同なので、対応する角の大きさや対応する辺の長さは等しいです。
角Aと角Dは対応する角なので等しい。よって、
角D=角A=35°
辺BCと辺EFは対応する辺なので、
辺EF=辺BC=6cm
よって答えは
角D=35°、辺EF=6cm
相似とは
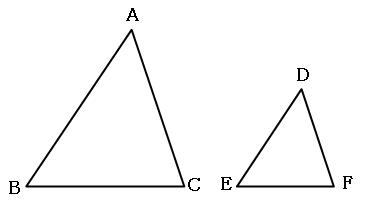
相似(そうじ)とは、形は同じだけど、大きさが違う図形のことです。
上の三角形ABCと三角形DEFは、形は同じですが、大きさが違うので相似です。「三角形ABCと三角形DEFは相似」といいます。
形は同じなので、対応する角の大きさは等しいです。が、大きさは違うので、対応する辺の長さは同じではありません。
ただし、一組だけ辺の比が分かれば、他の組の辺の比も同じ比になります。
例えば、AB:DE=a:bならば、BC:EF=a:bですし、AC:DF=a:bになります。
このような比を、相似比といいます。
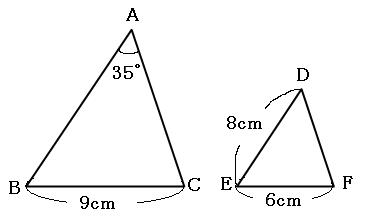
角Aと角Dは対応する角なので、
角D=角A=35°
続いて、対応する辺を見ていきましょう。対応する辺の組で、どちらも長さがわかっているのは、辺BCと辺EFの組です。その比を求めると、
辺BC:辺EF=9cm:6cm=3:2
よって、ふたつの三角形の相似比は3:2です。これで、他の2組の辺の比も3:2であることがわかったので、辺ABと辺DEを見比べて、
3:2=a:8cm
2×a=24
a=12
(比例式の解き方)
よって、辺ABの長さは12cm。 よって答えは
角D=35°、辺AB=12cm
相似の問題では、相似比をもとにして比例式を作って計算していくことが多くなります。 合同に比べて、いろいろな問題のパターンがあるので、テストでも聞かれやすいです。それでは合同と相似をまとめます。
次のページでは、相似をもう少し実践的に使えるようにします。
- 受験生応援オリジナルグッズ

エデュサポオリジナル受験生応援グッズ販売中!
エデュサポオリジナル受験生応援グッズをSUZURIにて販売しています。受験勉強のお供にお役立てください。頑張れ受験生!!